【帯域とは】帯域と通信速度 知ってるようで知らないキーワード解説

一般的に“帯域”という言葉は良く使われますが、その意味は理解していますか？何となく通信速度の意味で使っている人が多いと思いますが、本当にそれが正しいかどうか深く考える人は少ないでしょう。本記事では通信速度および帯域について説明します。少し物理や数学寄りのマニアックな内容になりますがお付き合い下さい。

通信速度について

帯域≒通信速度でOK

まずは結論として、帯域と通信速度はほぼ同じ意味で使ってOKです。超厳密な意味では違う部分がありますが、少なくても普段の会話レベルでは実質同じです。そもそもどういった意味なのか、という点はこの記事で詳しく解説します。

通信速度とは

まず、通信速度とは何でしょうか。これは言うまでもなく一定時間にどれだけの情報量を遅れるかという数字です。

例えば1秒間に

• 吾輩は猫である。 

と送るのと

• 吾輩は猫である。名前はまだ無い。 

と送る場合では、後者の方がたくさんの情報（文字数）を送っているので通信速度は速いです。

デジタル世界での通信速度

もう少しデジタルな視点での通信速度について考えてみましょう。デジタル世界での情報（データ）はbit、つまり2進数で表現されす。2進数は0or1で表現される数字です。

2進数については以下記事を参照してみて下さい。

例えば1秒間に

• 1101と送ったら→4[bits per second]
• 1101000111と送ったら→10[bits per second]

となります。簡単ですね。bits per secondは長いのでbpsと略します。これがデジタル世界における通信速度の単位です。

因みに×1000をkと書くので、1000bps≒1kbps となります。

ピッタリ＝にならないのは理由があって、正確には1024bps=1kbpsです。私達が普段使う10進数ではk=×1000ですが、2進数の世界ではk=2¹⁰=1024です。とは言え細かい数字の話なので2進数であっても便宜上k=×1000にしてしまうことも多々あります。

“帯域”の詳細説明

ではいよいよ帯域の具体的な説明です。結論としては冒頭の通り、帯域≒通信速度です。かなり物理や数学っぽい話なので結論だけ知りたい人は最後のまとめだけ確認でも大丈夫です。

※注意：この記事は説明の便宜上、かなり簡易的なモデルに落とし込んでいます。実際の通信機器は複雑な処理をしていますが、あまり難解な話をしても意味も無いですから、そういった前提で見て頂けると幸いです。

周波数と測定周期で通信速度は決定する

通信で必要な事は相手に0or1の情報を送ることです。例えばこんな信号を考えてみます。高校物理で良くあるSIN（サイン）とかCOS（コサイン）とかのアレです。

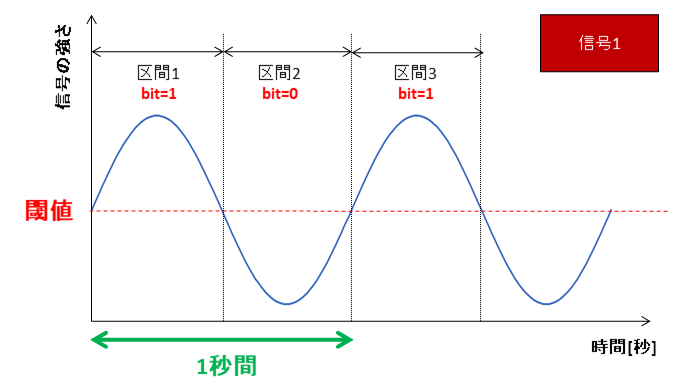
この信号は次の性質を持っています。

グラフを見ると、

• 区間1：閾値よりも信号が強いのでbitは1
• 区間2：閾値よりも信号が弱いのでbitは0

となります。至ってシンプルな話です。

区間1＋区間2で1秒間かつ2bit分表現されるため、通信速度は2[bps]です。

また、1秒間に波が何周するかを表す数字を周波数と言います。単位は[Hz](ヘルツ) です。この例だと1秒間に1周しているので1[Hz]です。

測定周期だけ短くしても通信速度は上がらない

測定周期を短くしたらどうなるか見てみましょう。信号1-1のグラフは測定周期を

0.5秒区間毎に測定
↓
0.25秒区間毎に測定

に変更したグラフです（信号1と波自体は同じで測定周期のみ変更）。

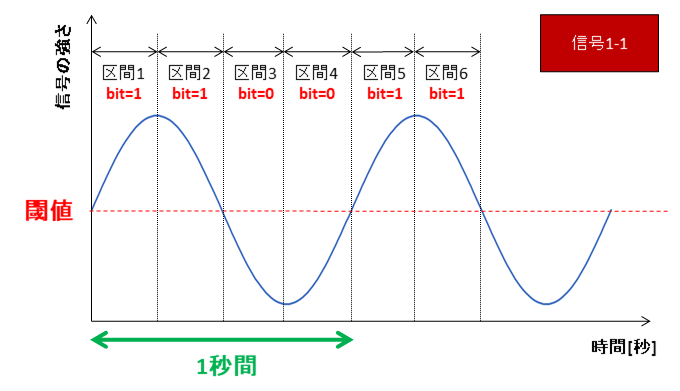
1秒間に4回測定するため2[bps]→4[bps]に倍増しました。

なので、測定周期をもっと短くすれば通信速度も速くなる・・・という単純な話ではないのです(*_*)

例えば本当に送りたいデータは

• 区間1=bit1
• 区間2=bit0

だったとします。それを表現するには区間1→区間2の0.25秒間で閾値よりも信号を弱くする必要がありますが、この信号はそんな急激には変化できないのです。（この例だと0.5秒かかる）

そのため測定周期だけを短くしても正確な情報を送れない以上、通信速度が上がったとは言えません。

信号の周波数も上がれば通信速度は向上

では通信速度を上げるためにはどうすれば良いでしょうか？答えは簡単でもっと急激に変化できる信号であればOKです。

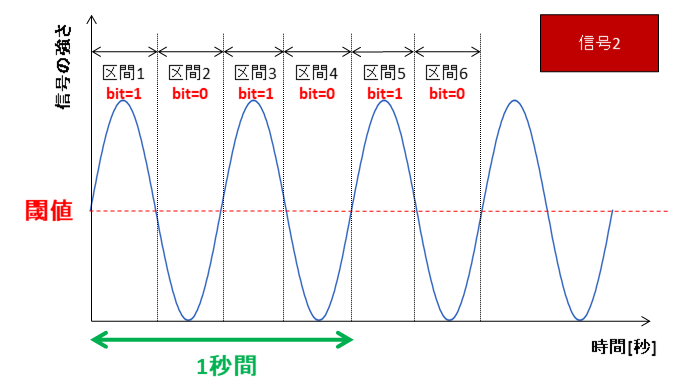
信号2は、周波数が信号1の2倍の2[Hz]です。これであれば0.25秒で1⇔0の変化ができるので、区間1=1→区間2=0という変化も正しく表現できます。

一方、

• 信号2：1→0→1→0・・・と規則正しい変化
• 実際の信号：1→1→0→1→0→0・・・と不規則な変化

であるためその点はもう少し考える必要がありそうです。

理想は方形波

では実際の信号はどういった波になるのでしょうか？先に理想形を出します。理想は信号3のようなある区間の切れ目で真上or真下に直角に変化する波です。これを方形波と言います。方形波は無駄のない0or1の信号で、正に理想的なデシタル信号です。

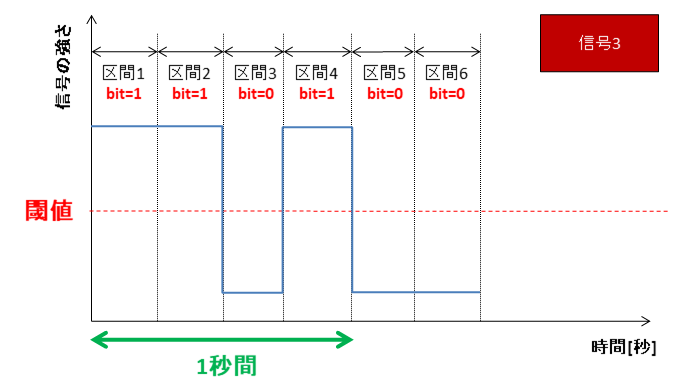
現実的には方形波は難しい

しかし、現実的には方形波を作る事は難しいです。なぜなら、

直角に変化する = 0秒で電気信号が変化する

と言う事だからです。電子部品の性能界的やノイズ等の理由で、現実的には信号4のような“近しい信号”になります。

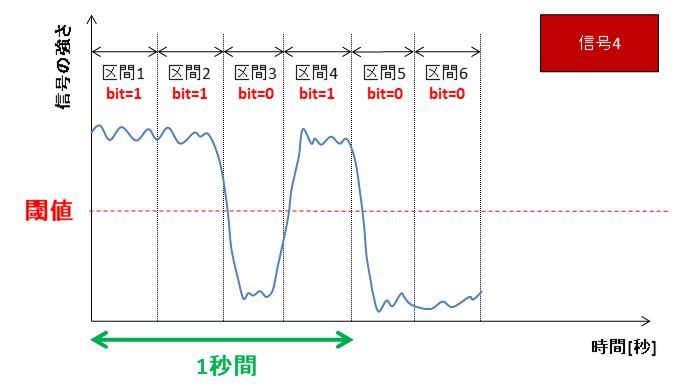
次からはこの近しい信号を作ることを考えます。

（電子機器で出力できるかは一旦置いておき）数学的に方形波は以下式で表現されます。
※数式を覚える必要はありません！

4 /𝜋 {𝑠in(𝑥) + 1/3𝑠in{3𝑥} + 1/5𝑠in(5𝑥) + ⋯}

“何でそうなるの？”という部分の詳細は割愛しますが、要は色々な周波数の波をたくさん足していくと出来上がる、という訳です。

例えば1[Hz]の信号と3[Hz]の信号と5[Hz]の信号と・・・とをたくさん合体させて行くと、信号4のような方形波っぽい波に段々と近づいて行きます。

時間軸と周波数軸で波を理解する

さて、忘れかけていますが帯域の話に少しずつ戻ります。

この“色々な周波数が混ざった波”は表現したい形に近づいていますが、波の形だけ見てもどういった周波数で構成されているかよく分かりませんよね。。。

波は“時間軸”および“周波数軸”両方から見ることで性質を理解することができます。

■時間軸のグラフ
横軸に時間[秒]を取り、時間の変化と共に信号の強さがどう変化したかを表現したグラフ

■周波数軸のグラフ
横軸に周波数[Hz]を取り、各周波数毎の信号の強さの分布を表現したグラフ

これは実際に見てみましょう。下記は信号1を例にした時間軸・周波数軸のグラフです。

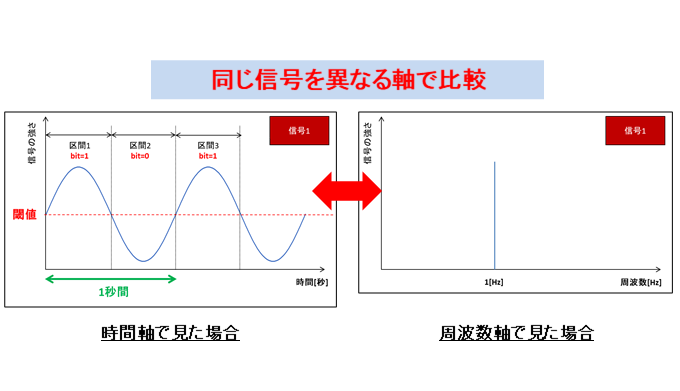
周波数軸のグラフは見慣れない形かもしれませんが、分かってしまえば理屈は簡単です。

複数の波を合体させても原理は同じ

上記は1[Hz]の例ですが、2[Hz]でも100[kHz]でも10[GHz]でも話は同じです。

では先程の“複数の周波数の波を合体させたパターン”を見てみましょう。一応グラフにするにあたっては以下式を想定しています。

𝑠in(𝑥) + 1/3𝑠in(3𝑥) + 1/5𝑠in(5𝑥) + 1/7sin(7x) + 1/9sin(9x)

まぁ細かい事は気にせず、とりあえず1[Hz] 、3[Hz]、5 [Hz] 、7[Hz] 、9 [Hz]の波の合体だと思って下さい。グラフは以下の通りです。

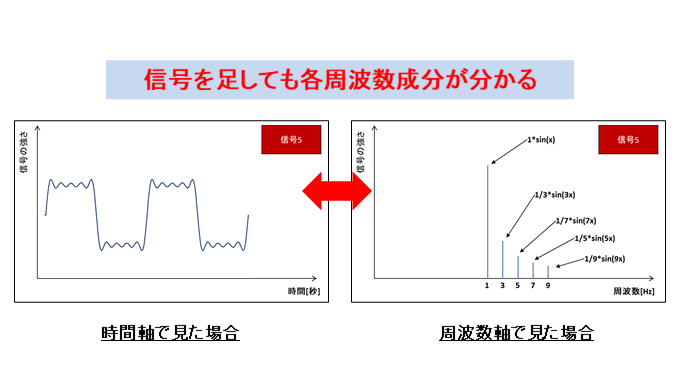
時間軸で見るとだいぶ方形波に近い形です。そして注目すべきは周波数軸のグラフの方で、見事に各周波数毎（1,3,5,7,9[Hz]）に分かれています。時間軸のグラフは見た目上混ざってしまい判別できませんが、周波数軸で見ると周波数毎に分かれるため一目で分かります。

ここでは1~9[Hz]の例で示しましたが、

更に高周波数成分を追加
↓
方形波に近づく
↓
より急激な変化を表現可能（通信速度が速なる）

となります。

一方、周波数は有限の値です。１つの信号が利用する周波数が多くなるとその分専有してしまい、他用途で利用できなくなります。このあたりはトレードオフの関係になります。

帯域とは

さて、この利用する周波数の幅のことを帯域幅（略して帯域）と言います。上記の例で言うと最大9[Hz] – 最小1[Hz]で帯域は8[Hz]です。

話としては、

色々な周波数の波をたくさん合体して使う（帯域をたくさん消費する）
↓
急激に変化する信号を作れる（方形波に近い波になる）
↓
短い時間にたくさんの情報を表現できる
↓
通信速度が速い

という原理です。

上記の『帯域をたくさん消費→通信速度が速い』の部分を繋げて、『帯域＝通信速度』 という意味合いで使われます。

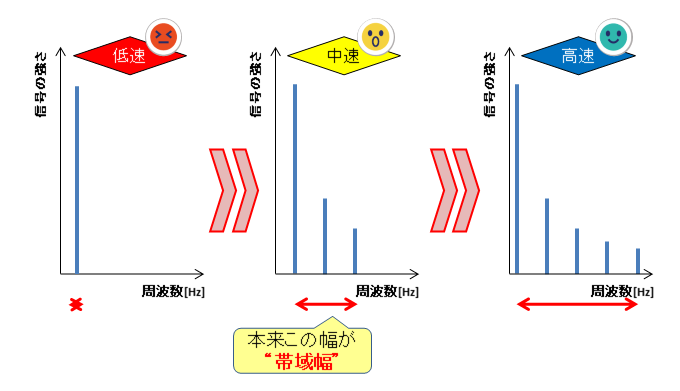
実際にはこんな、周波数成分があーだこーだと言う話は複雑なので、普段は『帯域が広い＝通信速度が速い』ということで問題ないかと思います。

一方、興味があればこういった話も調べると見識が広がるので気になったものは何でも調べてみると良いでしょう。

ネットワークエンジニアを目指すならCCNAを取得しよう！

CCNAとはCisco社のメーカ認定資格です。CCNAの取得はネットワークエンジニアの基本的な知識やCisco製品の理解の証明になります。

Ciscoは数あるネットワーク機器メーカの内の1社ですがディファクトスタンダードと言われています。つまり業界標準として位置付けられており、他メーカ機種でもCiscoのコマンドライン等を参考にしている事が多いです。そのため初見の機器でもCiscoと設定方法が似ており、「大体は分かる」なんてケースも多々あります。ネットワークエンジニアとしてはCiscoの学習はむしろ必須と言えるレベルでしょう。

また、Ciscoの資格と言っても独自仕様や製品の話だけでなく、ネットワークの一般的な知識も必要です。Cisco製品と言えベースはネットワークの標準規格に基づいて設計されており、CCNA取得でネットワークの一般的な知識も習得可能です。

上記理由からCCNAは非常におすすめの資格です。ネットワークエンジニアとして本格的に活躍したいのであれば是非チェックすべきでしょう。

【CCNAとは】難しい？勉強は？Cisco資格の登竜門 基本解説

【CCNAとは】難しい？勉強は？Cisco資格の登竜門 基本解説

まとめ

今回は通信の世界でよく言われる帯域について説明しました。内容的には数学や物理の授業っぽい話に終始してしまい、耐性がないとキツイ（？）かもしれませんが知っていて損はないと思います。この記事では通信速度の話にフォーカスしましたが、その他よく言われるのが無線の話です。携帯キャリアのプラチナバンドだったり、Wi-Fiの周波数帯域等でも帯域（周波数）の話は出てくるので概要としてどんな話なのかだけでも把握しておきましょう。